人工生命
人工生命とは何のことか。
遺伝子組み替えで、人間が作った自然界にいない生物のことか・・・？
この分野の開拓者たちの足跡を見てみよう。
人工生命の開拓者たち
フォン・ノイマン
数理学者（ハンガリー人）
●ノイマン型コンピューターの原理
今日のコンピューターの基礎となる論理的アイデア「ゲームの理論」を考え出したのが、ノイマンである。ハンガリー生まれの数学者で、ドイツを経てアメリカに移住し、数理全般に画期的な業績を残した。
●オートマトンの原理
コンピューターを考え出した、ノイマンは「生命とは情報のプロセスにすぎない」と言う。（１９５７年）
情報処理のプロセスを持つ機械は生命現象のような振る舞いをし、自己増殖も可能だと考えた。
ノイマンのアイデアは（同僚の数学者スタニスラウ・ウラムのアドバイスを入れて）、格子上に石を並べて行くような論理ゲームで、格子を細胞（セル）に見立てれば、セル自身が自分自身の状態を変化させていく自動機械（セル・オートマトン）であった。
「ある格子の状態を、まわりの格子の状態に一定の論理規則を当てはめることで、次の状態に自動変換され、この操作が無限に繰り返されていく。」
ジョン・ホートン・コンウェー
数学者（イギリス人）
●コンウェー集合
２０代前半で、ケンブリッジ大学で地位を得、その後集合数論の分野で「コンウェー集合」と呼ばれる大発見をした。その後、彼は数論の分野でやるべきことが見えなくなっていた。
●ライフゲーム
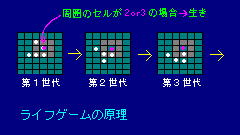セルオートマトンの研究に関心を持った。彼はノイマンの考えをよりを単純化し、時間ごとにチェス盤の上で人間が更新出来るよな基本的なセルオートマトンを作ろうと考えた。その鍵になるのは、生存や誕生や死を支配する規則だった。
１つのセルはその周囲に８つのセルと接している。
Ａ：あるセルがチェス盤上で生きているとき
- １：周囲の８セルの内、２または３個生きている場合、次の時間ステップ（世代）で生き残る。
- ２：周囲の８セルの内、４つ以上生きている場合、人口過剰で死ぐ。
- ３：周囲の８セルの内、生きているのが１つ以下では、露出しすぎで死ぐ。
Ｂ：あるセルがチェス盤上で死んでいるとき
- １：周囲の８セルの内、ちょうど生きたセルが３つの時誕生するが、そのほかの場合は死んだまま。
規則はこれだけである。コンウェーと友人たちでこのライフゲームは始まった。
スティーブン・ウォルフラム
●セルオートマトンの研究
子供の頃から数学と物理学に興味を持ち、１６才でオクスフォード大学に入学する天才少年だった。
２０才で博士号を取得し研究員の地位を得たが、自分で書いたコンピューターのシンボル操作原語の所有権を巡って喧嘩となり、カリフォルニア工科大学を去ることになった。
次に選んだ行き先は、昔アインシュタインやフォン・ノイマンがいたプリンストン高等研究所で、驚くことに素粒子物理理学をあっさり捨ててセルオートマトンの研究をはじめたのである。
彼がセルオートマトンに興味を持ったのは、容易にコンピューターの中で実行できる本物の「複雑系」であることだった。単純な起源から複雑さが生じる現象（＝複雑系）を表現するのに使えると考えた。
●１次元のセルオートマトン
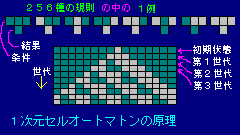ウォルフラムは、単純に見えることから始めそこから非常に複雑なものが出てくると考えていた。この主張を明確にするため、彼は１次元のセルオートマトンというを考えた。
１次元のセルオートマトンは水平方向に１列の線上に展開される。１つのセルは左右２つのセルとしか接触しないが、次の世代を下方に重ねて表現できるため、その履歴が一目で分かる利点がある。
- 規則はあるセルとその左右の計３つセルのON/OFF状態が、その次世代セルのON/OFFを決めるというもの。
- ３つのセルの状態は２ｘ２ｘ２＝８通りある。
- 規則の決め方は８ｘ８ｘ８＝２５６通りある。
●４つのクラス
彼は２５６通りの規則の決め方（規則群）を全部調べてみた。その結果、ある法則性の存在に気づき、４つのクラスに分類した。
クラス１：世代を経るうちに、全体がONまたはOFFになる場合。
クラス２：最初はバラバラな動きをするが、ある安定した模様に落ち着く場合。
クラス３：いつまでもON/OFFがランダムな模様となって出現する場合。（カオス）
クラス４：ランダムな動きをしたかと思えば、何世代か後に突然意味ありげな模様を生成したりする場合。
１９８２年、「クラス４」の発見は、ライフゲームの規則群を含む万能コンピューターとしての領域であった。後に「複雑適応系の生息領域」として注目を集めることになることになる。
クレイグ・レイノルズ
コンピューター会社のアニメ部門で仕事をしていたレイノルズは、コンピューターの中で動物の群れる振る舞いを与えるプログラムを考えていた。
彼は近くの墓地に群れるカラスの観察に通い詰めた。鳥たちが急に飛び立ち群れを形成していく様は、指揮官が笛を吹いているかのようにみえるが、しかし、群れの行動を命令している鳥はいなくてそれぞれの鳥は何か簡単な規則に従っている、と彼は考えた。そして、３つの規則にたどり着いた。
●群れる鳥のシュミレーション
１：近くの鳥たちが数多くいる方へ向かって飛ぼうとする。
２：近くにいる鳥たちと、飛ぶ速さと方向を合わせようとする。
３：近くの鳥や物体に近づきすぎたら、ぶつからないように離れようとする。
３つの規則で作った鳥のシュミレーションモデル「ボイド」は、予想以上に自然な振る舞いをして見せた。この手法は改良され、現在アニメーションや映画の実写合成ＣＧとして応用されている。
クリストファー・ラングントン
●不思議な体験
病院の仕事の後、いくつかの職につく間に科学への興味が高まり、ボストン大学で数学と天文学の聴講を受け始めた。１９９５年、親しくなった教師の薦めでアリゾナ大に入学し天文学の勉強をはじめた夏、ハンググライダーに夢中となり、その練習中に墜落事故で入院。記憶が一部失われ、１４回もの整形手術を受けた。毎日目が覚めるたびに、少しずつ記憶が甦り「自分の一部が戻ってくる」感覚を経験する。それはあたかもコンピューターの立ち上がりのような感覚であったという。
●人工生命へ
リハビリしながらのアリゾナ大学での天文学は、それほど興味のあるものとはならずそのころ発売されたパソコン・アップルUを入手し、１９９７年図書館で見つけたノイマンの論文「セルオートマトン」との格闘が始まった。研究の末、セルオートマトンのループ（環状セル）を自己複製させることに成功した。卒業が迫っていたので、研究成果をもって研究室周りをしたが、受け入れられずアリゾナ大大学院への希望は絶たれた。ところが、１９８２年ミシガン大学が彼を３３才の院生として受け入れたのであった。
●λ(ラムダ)パラメーター
ミシガン大学１年の時、セルオートマトンを４つのクラスに分類したウォルフラムの論文を読んでビックリした。彼は「ウォルフラムの４つのクラス」に内在する関係の研究に着手した。
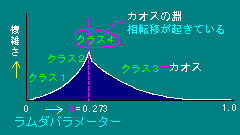
彼の考えたλパラメーターとは、セルオートマトンの振る舞いが小さいときλ＝０，大きいときλ＝１の値を取る。分子の状態で説明すれば、λ＝０：個体／λ＝１：気体といったイメージとなる。
「ウォルフラムの４つのクラス」を当てはめると、
λ＝０＜クラス１＜クラス２＜クラス４＜クラス３＜λ＝１
そして、ライフゲームのような生命と同じ様な振る舞いをする場合
λ＝0.273（クラス４）の値を取った。
●相転移・・・カオスの淵
クラス４の状態は、ちょうど個体が液体に相転移するλ値として理解できた。
さらに、「λ値」を横軸、「情報理論でいう複雑さ」を縦軸にしてみるとはっきりとした特徴が現れた。ラングストンは、この領域を「カオスへの転移」「カオスの境界」と呼んでいたが、後にパッカードの銘々した「カオスの淵」が一般化した。
トム・レイ
●生物学者として
トム・レイはハーバード大学大学院で生物学で学位を取得した後、１６年間コスタリカの熱帯雨林でフィールド・ワークに従事した。そして、進化が生む多様性の謎を解明したいと考えていた。
大学院時代、ケンブリジ囲碁クラブでそのルールを教えてもらったときのことであった。「生き石、死に石」の説明を聞き、「囲碁は自己増殖するプログラム」との比喩がこころにひっかかった。この仕組みがコンピューターで上手に生かされれば、進化システムを構築して自然淘汰の実証ができると直感し、興奮を覚えた。
●コンピューター・ウイルス
熱帯雨林の研究で一応の成果を得てデラウｪア大学の助教授となった時、長い間忘れていた「自己増殖するプログラム」の記憶が突然蘇ってきた。彼はじっとしていられなくなり、こうした分野に興味がある仲間がいない探しはじめた。ネットワークに質問を流し、そして1987年の第１回人工生命会議の論文集にたどり着いた。
レイのアイデアは「コンピューターのメインメモリーに棲息し、シリコンの領土を奪い合うコンピューターの命令から成る生物を作ること。」だった。
ラングトンやファーマーと相談した結果、コンピューターの中に仮想のコンピューターを作り、その中でしか生きられない生物にすべきだと提案を得た。１９８８年にインターネットに出現した「ワーム」と違い、進化するウイルスはさらに破壊的なものになる危険があったからだ。
●ティエラ（人工的環境）の設計
レイはデジタル生物の環境を、種が爆発的に増えたカンブリア期（約６億年前）に設定した。
- デジタル生物は仮想ＣＰＵ内のメモリー「スープ」（と銘々）上に、遺伝子型のコードで作られ、ＣＰＵ時間がくるごとに細胞分裂、増殖する。
- 生物に死を与える方法は、別々の直線上に並んだ生物をその列の先頭から消去する「刈り手」を考えた。一般的には年をとって前列に来たものだ。スープの８０％が埋め尽くされた時、「刈り手」の仕事開始とした。
- 宇宙線によって起こる突然変異に等しいものとして、増殖時に突然、コードのピットがひっくり返る方法を導入した。最後に、生物が命令を実行した時、命令をランダムに変えていしまう突然変異も用意した。
●ティエラの誕生
1990年１月３日、「大祖先」と呼ぶ最初の生物は、８０の命令で出来たものから始まった。
- 最初、８０命令の生物から７９命令の種族が出現した。
- 次に、生物はさらに小さくなり、ついに４５命令の「寄生者」が現れる。完全なコードを持つ宿主は寄生者に駆逐されると、今度は借りるコードを失った寄生者は、周期的に大混乱に陥った。
- こんどは、宿主のなかで寄生者の攻撃から身を守る「免疫性」を持った生物が現れ、寄生者を一掃してしまった。
- また、やや大きいコード数の「新種の寄生者」が出現。
ティエラは即座に結果を描き出し、レイは一気に人工生命研究の先頭に立つこととなった。
人工生命研究の成果
「人工生命」とは人間によって作られた生命現象であるが、その定義は明確ではない。この研究はまだ始まったばかりで、１９８７年最初に開催された国際会議から認知されたばかりの研究分野です。それが、どんな方向に向かって発展してきたかを見てきました。
●人工生命研究の意義
人工生命の名付け親であるラングストンは、
「人工生命は、自然の生命系に特有の振る舞いを示す人工的なシステムについての研究である。これは生命というものを、地球に生じた特別な例に限定せず、可能な限りの表現を通して説明しようとするものである。（中略）究極の目標は、生命系の論理形式を抽出することである。」
生物的な振る舞いの一部を複製する事で、生命出現の謎を解明できるかもしれない。今後の成果に期待したい。
●遺伝的アルゴリズム
最近、理工学の分野で「遺伝的アルゴリズム（ＧＡ＝Genetic Algorithms）」を使った応用研究が盛んになってきました。コンピューターを使ったデーター処理でも、巨大なデーターになるとお手上げになります。そこで、もう少し短時間に「最適解を検索できないか・・・」という研究分野に登場したのがＧＡの手法です。
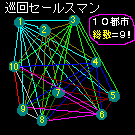有名な例としては「巡回セールスマン問題」があります。
たとえばセールスマンが１０の都市を１回ずつ訪問する最小コスト（＝最短距離としておきます）の経路or順番を求める問題です。
最適解を計算するには、全組合わせを検索すれば答えが出ますが
都市の数を増やしていくと、飛躍的に計算総数は増加していきます。
各都市を巡回する組合せ総数は、
・ ５都市で 4！＝1x2x3x4＝24通り
・１０都市で 9！＝1x2x3x4x5x6x7x8x9＝約 36万通り
・１５都市で 14！＝1x2x3x4x5x6x7x8x9x10x11x12x13x14＝約872億通り
・２０都市で 19！＝1x2x3x4x5x6x7x8x9x10x11x12x13x14x15x16x17x18x19＝約872億x140万通り
わずか２５〜３０都市で、コンピューターの処理にも限界が現れます。
遺伝的アルゴリズム（ＧＡ）とは生物進化モデルの仕組みを使って、問題解決に利用する手法です。
巡回セールスマン問題の計算手法（アルゴリズム）は下記のようになります。
・問題解決に適した遺伝子（染色体）モデルを設定する。
・モデルを評価する仕組みをつくる。（巡回経路の合計が短いほど良い）
・モデルを生き残らせる基準値（or生存率）を決める。
- 初期モデルをランダムに発生させる。
- 評価が基準に達していない個体に「死」を与える。
- 生き残った個体を交配し、新たな染色体を持つ個体を生成する。
- 低い確率でランダムに選んだ遺伝子が突然変異を起こした個体をつくる。
- [2]に戻る。（世代数＝世代数＋１）
モデルの設計が適切だと、短時間（世代数）で最適解に達することが可能です。
このあたりは、具体的な研究の分野でしょう・・・。
▼参考文献
- スティーブン・レビー著（服部桂訳）「人工生命」1996、朝日新聞社
- 吉永良正著「「複雑系」とは何か」1996、講談社
- 長久勝著「遺伝的アルゴリズム」1999、Ｃマガジン1999年９月号、ソフトバンク
Return
